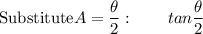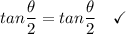Answer: see proof below
Explanation:
Use the following Double Angle Identities:
sin 2A = 2cos A · sin A
cos 2A = 2 cos²A - 1
Use the following Quotient Identity: tan A = (sin A)/(cos A)
Use the following Pythagorean Identity:
cos²A + sin²A = 1 --> sin²A = 1 - cos²A
Proof LHS → RHS
Given:
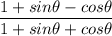
Let Ф = 2A:
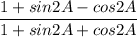
Un-factor:
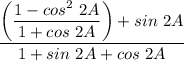
Pythagorean Identity:
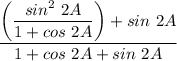
Simplify:
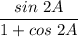
Double Angle Identity:
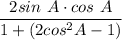
Simplify:
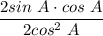
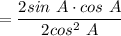
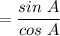
Quotient Identity: tan A