Question

A magnitude 6.7 earthquake struck the SanFernando valley region of Los Angeles in 1994, causing widespread damage. Suppose another region with more active earthquakes and the number of earthquakes in this region is a random variable (binomial) distribution. Use a normal distribution approximation to find standard deviation if the probability is 0.87 that there will be at least 15 earthquakes with mean=17.6.

Answer 1

Answer: 2.308 .

Explanation:

Let X denotes the number of earthquakes in SanFernando valley region of Los Angeles in 1994.

Given:
`\mu=17.6`

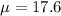
Probability is 0.87 that there will be at least 15 earthquakes .

i.e.
`P(X\geq15)=0.87`

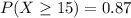
`\Rightarrow\ P((X-\mu)/(\sigma)\geq(15-17.6)/(\sigma))=0.87\\\\ \Rightarrow\ P(Z\geq(-2.6)/(\sigma))=0.87\ \ \ [Z=(X-\mu)/(\sigma)]`

Z-value corresponding to p-value 0.87 is -1.1263 .

So,
`(-2.6)/(\sigma)=-1.1263`

`\sigma= (-2.6)/(-1.1263)\approx2.308`

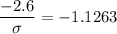
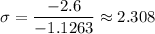
Hence, the required standard deviation = 2.308 .