Answer:
119.45 m
Explanation:
Given:
When angle of elevation of the sun changes from 58° to 36° the length of shadow of a pole increases by 90 m.
To find:
Length of pole = ?
Solution:
Kindly refer to the attached image.
 represents the 1st angle of elevation of sun i.e. 58°
represents the 1st angle of elevation of sun i.e. 58°
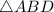 represents the 2nd angle of elevation of sun i.e. 36°
represents the 2nd angle of elevation of sun i.e. 36°
Change in shadow is represented by CD = 90 m
Let height of pole, AB =
 m
m
Let side BC =
 m
m
Now, let us apply tangent rules in
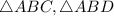 one by one:
one by one:

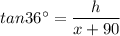
Putting value of
 using equation (1):
using equation (1):
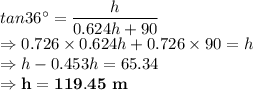
119.45 m is the height of pole.