Question

**Please Help, ASAP**

Rearrange the formula so the letter in parenthesis is the subject. Show your work as well.
1) x+xy = y, (x)
2) x+y = xy, (x)
3) x = y+xy, (x)
4) E = (1/2)mv^2-(1/2)mu^2, (u)
5) (x^2/a^2)-(y^2/b^2) = 1, (y)
6) ay^2 = x^3, (y)

Answer 1

Step-by-step explanation:

We need to rearrange the following formula for the values given in parenthesis.

(1) x+xy = y, (x)

taking x common in LHS,

x(1+y)=y

`x=(y)/(1+y)`

(2) x+y = xy, (x)

Subrtacting both sides by xy.

x+y-xy = xy-xy

x+y-xy = 0

x-xy=-y

x(1-y)=-y

`x=(-y)/(1-y)`

(3) x = y+xy, (x)

Subrating both sides by xy

x-xy = y+xy-xy

x(1-y)=y

`x=(y)/(1-y)`

(4) E = (1/2)mv^2-(1/2)mu^2, (u)

Subtracting both sides by (1/2)mv^2

E-(1/2)mv^2 = (1/2)mv^2-(1/2)mu^2-(1/2)mv^2

E-(1/2)mv^2 =-(1/2)mu^2

So,

`2(E-(1)/(2)mv^2)=-mu^2\\\\u^2=(-2)/(m)(E-(1)/(2)mv^2)\\\\u=\sqrt{(-2)/(m)(E-(1)/(2)mv^2)}\\\\u=\sqrt{(2)/(m)((1)/(2)mv^2-E)}`

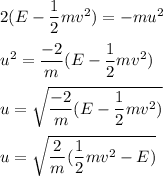
(5) (x^2/a^2)-(y^2/b^2) = 1, (y)

`(x^2)/(a^2)-1=(y^2)/(b^2)\\\\y^2=b^2((x^2)/(a^2)-1)\\\\y=b\sqrt{(x^2)/(a^2)-1}`

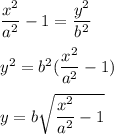
(6) ay^2 = x^3, (y)

`y^2=(x^3)/(a)\\\\y=\sqrt{(x^3)/(a)}`

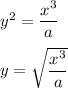
Hence, this is the required solution.