Answer:
definite integral I = 0.001591 to six decimal places
Explanation:
The definite integral is given as:

For arctanx , the power series is in the order
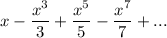
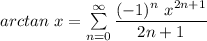
The next step is to substitute the value of 5x for x in the above equation;
So,
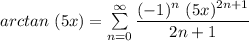
To multiply both sides by (x); we have
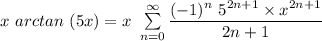
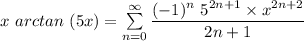
Taking the integral on both sides with respect to x;
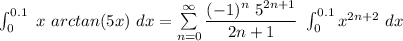
![\int^(0.1)_(0) \ x \ arctan (5x) \ dx = \sum \limits ^(\infty)_(n=0) ((-1)^n \ 5^(2n +1))/(2n+1) \ [(0.1)^(2n+3)]](https://img.qammunity.org/2021/formulas/mathematics/college/rmyww379wrnuwvlgui1dkzpoejwugal4zk.png)
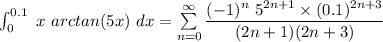
![\int^(0.1)_(0) \ x \ arctan (5x) \ dx = [(5 * (0.1)^3)/(1.3)-(5^3(0.1)^3)/(3.5)+(5^5(0.1)^7)/(5.7)-(5^7(0.1)^9)/(7.9)+ ...]](https://img.qammunity.org/2021/formulas/mathematics/college/gihr84clefelwkmyzptrcpzhmpa2k14nvy.png)
![\int^(0.1)_(0) \ x \ arctan (5x) \ dx = [(1)/(600)-(1)/(1200)+(1)/(112000)-(1)/(806400)+ ...]](https://img.qammunity.org/2021/formulas/mathematics/college/tfxbragfgzgccppozyihwtrsrdhtm530po.png)
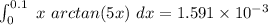
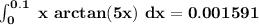 to six decimal places
to six decimal places