Question

Use a power series to approximate the definite integral, I, to six decimal places. 0.1 x arctan(5x) dx 0.

Answer 1

definite integral I = 0.001591 to six decimal places

Explanation:

The definite integral is given as:

`\int ^(0.1)_(0) \ x \ arctan (5x) \ dx`

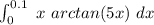
For arctanx , the power series is in the order
`x - (x^3)/(3)+ (x^5)/(5)-(x^7)/(7)+...`

`arc tan \ x = \sum \limits ^(\infty)_(n=0) ((-1)^n \ x ^(2n+1))/(2n +1)`

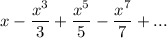
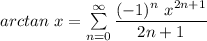
The next step is to substitute the value of 5x for x in the above equation;

So,

`arc tan \ (5x) = \sum \limits ^(\infty)_(n=0) ((-1)^n \ (5x) ^(2n+1))/(2n +1)`

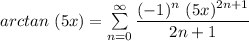
To multiply both sides by (x); we have

`x\ arc tan \ (5x) = x \ \sum \limits ^(\infty)_(n=0) ((-1)^n \ 5 ^(2n+1) * x^(2n+1))/(2n +1)`

`x\ arc tan \ (5x) = \sum \limits ^(\infty)_(n=0) ((-1)^n \ 5 ^(2n+1) * x^(2n+2))/(2n +1)`

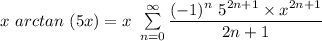
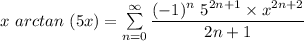
Taking the integral on both sides with respect to x;

`\int^(0.1)_(0) \ x \ arctan (5x) \ dx = \sum \limits ^(\infty)_(n=0) ((-1)^n \ 5^(2n +1))/(2n+1) \ \int ^(0.1)_0 x^(2n+2) \ dx`

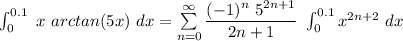
`\int^(0.1)_(0) \ x \ arctan (5x) \ dx = \sum \limits ^(\infty)_(n=0) ((-1)^n \ 5^(2n +1))/(2n+1) \ [(0.1)^(2n+3)]`

`\int^(0.1)_(0) \ x \ arctan (5x) \ dx = \sum \limits ^(\infty)_(n=0) ((-1)^n \ 5^(2n +1) * (0.1)^(2n+3) )/((2n+1)(2n+3))`

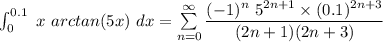
`\int^(0.1)_(0) \ x \ arctan (5x) \ dx = [(5 * (0.1)^3)/(1.3)-(5^3(0.1)^3)/(3.5)+(5^5(0.1)^7)/(5.7)-(5^7(0.1)^9)/(7.9)+ ...]`

`\int^(0.1)_(0) \ x \ arctan (5x) \ dx = [(1)/(600)-(1)/(1200)+(1)/(112000)-(1)/(806400)+ ...]`

`\int^(0.1)_(0) \ x \ arctan (5x) \ dx =1.591 * 10^(-3)`

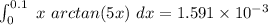
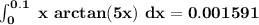`\mathbf{\int^(0.1)_(0) \ x \ arctan (5x) \ dx =0.001591}` to six decimal places