Question

The weight load on an airplane pallet is normally distributed with a mean of 250 pounds and a standard deviation of 40 pounds. What is the probability that a randomly selected pallet will support more than 290 pounds

Answer 1

Answer: 0.1587

Explanation:

Given : The weight load on an airplane pallet is normally distributed with a mean of 250 pounds and a standard deviation of 40 pounds.

i.e.
`\mu = 250` pounds

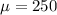`\sigma=40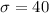` pounds

Let x be the weight load on an airplane pallet.

Then, the probability that a randomly selected pallet will support more than 290 pounds will be :-

`P(X>290)=P((X-\mu)/(\sigma)>(290-250)/(40))\\\\=P(Z>1)\ \ \ \ [z=(X-\mu)/(\sigma)]\\\\=1-P(Z<1)\\\\=1-0.8413\ \ \ \ [\text{by z-table}]\\\\=0.1587`

Hence, the required probability is 0.1587 .