Question

The overhead reach distances of adult females are normally distributed with a mean of 205.5 cm and a standard deviation of 8.6 cm

a. Find the probability that an individual distance is greater than 214.80 cm.
b. Find the probability that the mean for 1515 randomly selected distances is greater than 204.00 cm
c. Why can the normal distribution be used in part​ (b), even though the sample size does not exceed​ 30?
a. The probability is
​(Round to four decimal places as​ needed.)
b. The probability is
​(Round to four decimal places as​ needed.)
c. Choose the correct answer below.
A. The normal distribution can be used because the original population has a normal distribution.
B. The normal distribution can be used because the probability is less than 0.5
C. The normal distribution can be used because the mean is large.
D. The normal distribution can be used because the finite population correction factor is small

Answer 1

The probability of an individual distance being greater than 214.80 cm is found using the z-score and the standard normal distribution table. The probability that the mean of 1515 distances is greater than 204.00 cm can be calculated due to the Central Limit Theorem. The normal distribution can be used in part (b) because the original population has a normal distribution.

Step-by-step explanation:

To find the probability that an individual distance is greater than 214.80 cm, we use the z-score formula:

Z = (X - μ) / σ

Where X is the value of interest (214.80 cm), μ is the mean (205.5 cm), and σ is the standard deviation (8.6 cm). Plugging in the values:

Z = (214.80 - 205.5) / 8.6 ≈ 1.081

We then look up this z-score in the standard normal distribution table to find the probability of a z-score being less than 1.081 and subtract it from 1 to find the probability of it being greater. The answer will be the required probability (a).

To address (b), we use the Central Limit Theorem which says that sampling distribution of the sample mean will be normally distributed if the sample size is large enough, typically n>30. Given that the sample size is 1515, which is greater than 30, we can use the normal distribution to calculate the probability.

In this case, we calculate the standard error (SE) using SE = σ / √n and then find the z-score for 204.00 cm using the new mean. We can then find the probability that the mean for 1515 randomly selected distances is greater than 204.00 cm by looking up the corresponding value in the z-table.

For (c), the correct answer is A. The original population distribution being normal allows us to use the normal distribution for the sample mean regardless of the sample size.

Answer 2

(a) the probability that an individual distance is greater than 214.80 cm is 0.1401.

(b) The probability that the mean for 15 randomly selected distances is greater than 204.00 cm is 0.2482.

(c) The normal distribution can be used because the original population has a normal distribution.

Step-by-step explanation:

We are given that the overhead reach distances of adult females are normally distributed with a mean of 205.5 cm and a standard deviation of 8.6 cm.

(a) Let X = the overhead reach distances of adult females.

The z-score probability distribution for the normal distribution is given by;

Z =
`(X-\mu)/(\sigma)` ~ N(0,1)

where,
`\mu` = population mean reach distance = 205.5 cm

`\sigma` = standard deviation = 8.6 cm

So, X ~ Normal(
`\mu=205.5,\sigma^(2) =8.6^(2)`)

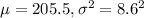Now, the probability that an individual distance is greater than 214.80 cm is given by = P(X > 214.80 cm)

P(X > 214.80 cm) = P(
`(X-\mu)/(\sigma)` >
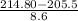`(214.80-205.5)/(8.6)` ) = P(Z > 1.08) = 1 - P(Z
`\leq` 1.08)

= 1 - 0.8599 = 0.1401

The above probability is calculated by looking at the value of x = 1.08 in the z table which has an area of 0.8599.

(b) Let
`\bar X` = the sample mean selected distances.

The z-score probability distribution for the sample mean is given by;

Z =
`(\bar X-\mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where,
`\mu` = population mean reach distance = 205.5 cm

`\sigma` = standard deviation = 8.6 cm

n = sample size = 15

Now, the probability that the mean for 15 randomly selected distances is greater than 204.00 cm is given by = P(
`\bar X` > 204.00 cm)

P(
`\bar X` > 204 cm) = P(
`(\bar X-\mu)/((\sigma)/(√(n) ) )` >
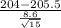`(204-205.5)/((8.6)/(√(15) ) )` ) = P(Z > -0.68) = 1 - P(Z
`\leq` 0.68)

= 1 - 0.7518 = 0.2482

The above probability is calculated by looking at the value of x = 0.68 in the z table which has an area of 0.7518.

(c) The normal distribution can be used in part​ (b), even though the sample size does not exceed​ 30 because the original population has a normal distribution and the sample of 15 randomly selected distances has been taken from the population itself.