The bases are the same, so we add the exponents
The answer is
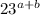 which is choice A
which is choice A
============================================
Here's an example of why we add the exponents
Lets say we want to multiply 7^2 with 7^3
7^2 = 7*7
7^3 = 7*7*7
We have two copies of "7" being multiplied with 7^2, then we have an additional three copies of "7" with 7^3. Overall there are 2+3 = 5 copies of "7" that we multiply out.
So,
7^2*7^3 = (7^2) * (7^3)
7^2*7^3 = (7*7) * (7*7*7)
7^2*7^3 = 7*7*7*7*7
7^2*7^3 = 7^5
This example is fairly small in that we don't have that many copies of the base being multiplied. For larger examples, its best to use the formula mentioned
a^b*a^c = a^(b+c)