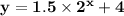Answer:
Explanation:
Given:
Exponential function with common ratio 2.
Horizontal asymptote at y = 4
Passes through point (2, 10)
To find:
Equation of the exponential function ?
Solution:
Equation for an exponential function may be given as:
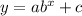
Where b is the common ratio and
c is the y value of horizontal asymptote.
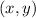 are the points on the function.
are the points on the function.
We are given that:
b = 2
c = 4
Let us put all the given values and find equation.
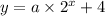
Now, let us put
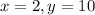 to find the value of a.
to find the value of a.
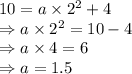
 the equation of exponential function is:
the equation of exponential function is: