Answer:
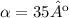
Explanation:
Primeiro, vamos dizer que essa folha tem extremidades nos pontos
.
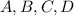E vamos chamar os vértices do triângulo que contém o ângulo
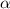de
.
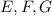Na semireta de baixo, formada por
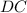, a gente tem um ângulo de
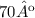e um outro ângulo de
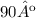(porque ele indica um ângulo reto).
Vamos dizer que estes dois ângulos se encontram no ponto
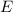, que combinamos antes, como vértice (extremidade) do triângulo de cima.
Como os dois ângulos, estão num mesmo ponto,
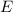, podemos dizer que existe um terceiro ângulo para o qual sua soma seja
. E tem, seria o ângulo à esquerda de
Vamos chamar este ângulo de
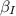. Portanto:
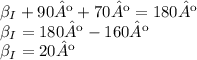
Agora, temos um outro triângulo no canto inferior esquerdo da folha, cujos ângulos são
,
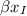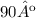e um outro ângulo, que vamos chamar de
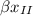
Esse último vai ser o ângulo superior deste triângulo, tá legal?
Então, vamos ter que:
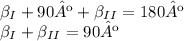
Como
,
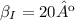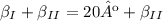
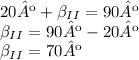
Ou seja, o ângulo superior do triângulo no canto inferior esquerdo, é 70º.
Vamos concordar, que este mesmo triângulo tem vértices nos pontos
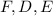. Onde
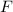é o ponto superior,
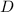é a extremidade inferior esquerda do retângulo e
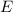é aquele mesmo ponto em que se encontram os ângulos d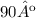e
e
.
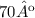Mais à frente, você vai entender o porquê é importante nomear estes pontos, eu fiquei 40 minutos tentando fazer essa questão sem fazer isso e não conseguia porque empacava numa parte da resolução.
Então, agora, sabemos que o ângulo
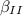, que é o encontro dos seguimentos
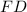e
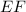vale
.
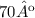Até aqui, foi só aplicar propriedades. Mas, a partir desse ponto, você vai precisar usar a criatividade.
Então, você entende que o ângulo
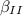está inserido numa reta com outros dois ângulos concentrados no ponto
.
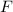Então, pode dizer que esse ângulo externo é o suplemento de
.
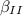Vamos chamar todo ele de
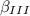
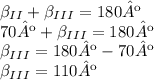
Agora, vamos elevar o nível de criatividade no raciocínio e ver também que temos um quadrilátero formado pelos pontos
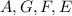
A soma dos ângulos de qualquer quadrilátero é 360º.
E temos que esse mesmo quadrilátero é formado por dois ângulos retos, além do ângulo de 110º que calculamos.
A última extremidade que falta é um ângulo formado pela soma de
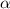a um outro ângulo, que vamos chamar de
.
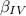Então, temos que:
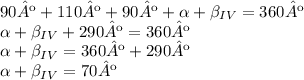
De todas, as etapas dessa resolução essa é a mais importante de entendermos os pontos que definimos. Eu refiz ela várias vezes porque não fiz isso antes.
Mas, veja, quando a gente dobra a folha, pegamos um formato qualquer e destacamos do resto dela.
Isso quer dizer que o formato que ficou dobrado é o mesmo que falta na folha. Do contrário, estaríamos criando folha ou excluindo matéria, o que não é possível no caso de uma simples dobra.
Em outras palavras, os triângulos
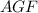e
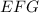são os mesmos. (Eu recomendo que você construa esse desenho e coloque as letras em cada ponto, pra visualizar melhor.)
Isso é o mesmo que dizer que os ângulos de um vão ser os ângulos do outro.
Portanto, os ângulos são equivalentes. (Mesmos ângulos para ambos os triângulos, mudando só de posição.)
Assim, você pode afirmar que
=
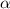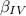
Se subirmos um pouco a resolução, vamos lembrar que encontramos que
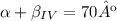
Se
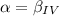
Temos:
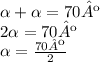
e TCHARAAN!
-------------------------
Força, guerreiro(a). Sucesso e que Deus te abençoe nos estudos.