Answer:
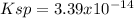
Step-by-step explanation:
Hello,
In this case, since the dissociation of gold (V) oxalate is:
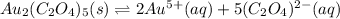
In such a way, the equilibrium expression is:
![Ksp=[Au^(5+)]^2[(C_2O_4)^(2-)]^5](https://img.qammunity.org/2021/formulas/chemistry/college/uwjkixnhjwnr2mt0cvix5xbnbmpvd1ft50.png)
Thus, since the molar solubility of the gold (V) oxalate is computed by considering its molar mass (834 g/mol):
![[Au_2(C_2O_4)_5]=2.58(g)/(L) *(1mol)/(834g) =3.09M](https://img.qammunity.org/2021/formulas/chemistry/college/vo62hmmnrjo501302xqx9izzi139x30wdh.png)
In such a way, since gold (V) is in a 2:1 molar ratio with the salt and the oxalate in a 5:1 in the chemical reaction, the corresponding concentrations at equilibrium are:
![[Au^(5+)]=3.09x10^(-3)(mol)/(L) *(2molAu^(5+))/(1mol) =6.19x10^(-3)M](https://img.qammunity.org/2021/formulas/chemistry/college/54e8ai9jl2pna9ge9wgwb9nyjohmvhsrvw.png)
![[(C_2O_4)^(2-)]=3.09x10^(-3)(mol)/(L) *(5mol(C_2O_4)^(2-))/(1mol) =0.0155M](https://img.qammunity.org/2021/formulas/chemistry/college/iv2e1hz3uu5aueeu044t1g5zso6wyg35s1.png)
Therefore, the solubility product turns out:

Regards.