Question

The solubility of gold (V) oxalate, Au2(C2O4)5 is 2.58 g/L. Calculate Ksp from this information.

Answer 1

`Ksp=3.39x10^(-14)`

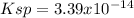
Step-by-step explanation:

Hello,

In this case, since the dissociation of gold (V) oxalate is:

`Au_2(C_2O_4)_5(s)\rightleftharpoons 2Au^(5+)(aq)+5(C_2O_4)^(2-)(aq)`

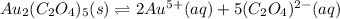
In such a way, the equilibrium expression is:

`Ksp=[Au^(5+)]^2[(C_2O_4)^(2-)]^5`

Thus, since the molar solubility of the gold (V) oxalate is computed by considering its molar mass (834 g/mol):

`[Au_2(C_2O_4)_5]=2.58(g)/(L) *(1mol)/(834g) =3.09M`

In such a way, since gold (V) is in a 2:1 molar ratio with the salt and the oxalate in a 5:1 in the chemical reaction, the corresponding concentrations at equilibrium are:

`[Au^(5+)]=3.09x10^(-3)(mol)/(L) *(2molAu^(5+))/(1mol) =6.19x10^(-3)M`

`[(C_2O_4)^(2-)]=3.09x10^(-3)(mol)/(L) *(5mol(C_2O_4)^(2-))/(1mol) =0.0155M`

Therefore, the solubility product turns out:

`Ksp=(6.19x10^(-3))^2*(0.0155)^5\\\\Ksp=3.39x10^(-14)`

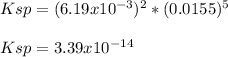
Regards.