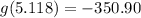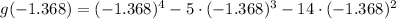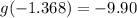Question

A graphing calculator is recommended. A function is given. g(x) = x4 − 5x3 − 14x2 (a) Find all the local maximum and minimum values of the function and the value of x at which each occurs. State each answer rounded to two decimal places.

Answer 1

The local maximum and minimum values are:

Local maximum

`g(0) = 0`

Local minima

`g(5.118) = -350.90`

`g(-1.368) = -9.90`

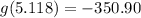
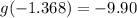
Explanation:

Let be
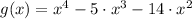`g(x) = x^(4)-5\cdot x^(3)-14\cdot x^(2)`. The determination of maxima and minima is done by using the First and Second Derivatives of the Function (First and Second Derivative Tests). First, the function can be rewritten algebraically as follows:

`g(x) = x^(2)\cdot (x^(2)-5\cdot x -14)`

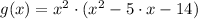
Then, first and second derivatives of the function are, respectively:

First derivative

`g'(x) = 2\cdot x \cdot (x^(2)-5\cdot x -14) + x^(2)\cdot (2\cdot x -5)`

`g'(x) = 2\cdot x^(3)-10\cdot x^(2)-28\cdot x +2\cdot x^(3)-5\cdot x^(2)`

`g'(x) = 4\cdot x^(3)-15\cdot x^(2)-28\cdot x`

`g'(x) = x\cdot (4\cdot x^(2)-15\cdot x -28)`

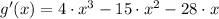
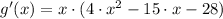
Second derivative

`g''(x) = 12\cdot x^(2)-30\cdot x -28`

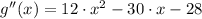
Now, let equalize the first derivative to solve and solve the resulting equation:

`x\cdot (4\cdot x^(2)-15\cdot x -28) = 0`

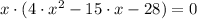
The second-order polynomial is now transform into a product of binomials with the help of factorization methods or by General Quadratic Formula. That is:

`x\cdot (x-5.118)\cdot (x+1.368) = 0`

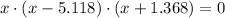
The critical points are 0, 5.118 and -1.368.

Each critical point is evaluated at the second derivative expression:

x = 0

`g''(0) = 12\cdot (0)^(2)-30\cdot (0) -28`

`g''(0) = -28`

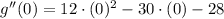
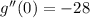
This value leads to a local maximum.

x = 5.118

`g''(5.118) = 12\cdot (5.118)^(2)-30\cdot (5.118) -28`

`g''(5.118) = 132.787`

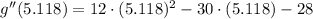
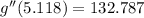
This value leads to a local minimum.

x = -1.368

`g''(-1.368) = 12\cdot (-1.368)^(2)-30\cdot (-1.368) -28`

`g''(-1.368) = 35.497`

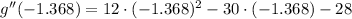
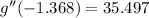
This value leads to a local minimum.

Therefore, the local maximum and minimum values are:

Local maximum

`g(0) = (0)^(4)-5\cdot (0)^(3)-14\cdot (0)^(2)`

`g(0) = 0`

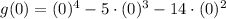
Local minima

`g(5.118) = (5.118)^(4)-5\cdot (5.118)^(3)-14\cdot (5.118)^(2)`

`g(5.118) = -350.90`

`g(-1.368) = (-1.368)^(4)-5\cdot (-1.368)^(3)-14\cdot (-1.368)^(2)`

`g(-1.368) = -9.90`