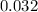Answer:
The point estimate = 0.507
Margin error of a given confidence interval = 0.032
Explanation:
The point estimate is calculated by using the sample statistics of a population.
Thus; point estimate can be expressed with the formula:
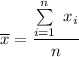
Given that : 0.475 < p < 0.539
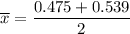
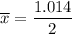
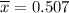
The point estimate = 0.507
The margin of error which shows the percentage of points that the derived results would differ from that of the given population value can be calculated with the formula:
Margin error of a given confidence interval =

Margin error of a given confidence interval =
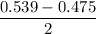
Margin error of a given confidence interval =
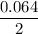
Margin error of a given confidence interval =