Question

Please help me as soon as possible ...​

Answer 1

Your question has been heard loud and clear.

tanθ+tan(60∘+θ)+tan(120∘+θ)

=tanθ+3–√+tanθ1−3–√tanθ+−3–√+tanθ1+3–√tanθ

[tanθ(1−3tan2θ)+(3–√+tanθ)(1+3–√tanθ)

=+(−3–√+tanθ)(1−3–√tanθ)1−3tan2θ

=9tanθ−3tan3θ1−3tan2θ=3tan3θ

Thank you.

Answer 2

Answer: see proof below

Explanation:

Use the following identities

tan (A + B) = (tan A + tan B)/(1 - tan A · tan B) -->
`(tanA+tanB)/(1-tanA\cdot tanB)`

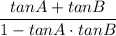
tan 60° = √3

tan 120° = -√3

tan 3A = (3tanA - tan³A)/(1 - 3 tan²A) -->
`(3tanA-tan^3A)/(1-3tan^2A)`

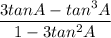
Proof LHS → RHS

Given: tan Ф + tan(60° + Ф) + tan(120° + Ф)

Sum Difference: tan Ф + (tan 60° + tanФ)/(1-tan60°·tanФ) + (tan 120° + tanФ)/(1-tan120°·tanФ)

(latex)
`tan\theta+(tan60^o+tan\theta)/(1-tan60^o\cdot tan\theta)+(tan120^o+tan\theta)/(1-tan120^o\cdot tan\theta)`

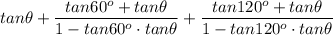
Substitute: tan Ф + (√3 + tanФ)/(1-√3·tanФ) + (-√3 + tanФ)/(1+√3°·tanФ)

(latex)
`tan\theta+(\sqrt3+tan\theta)/(1-\sqrt3 tan\theta)+(-\sqrt3+tan\theta)/(1+\sqrt3tan\theta)`

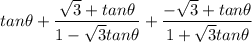
Common Denominator: [tan Ф(1-3tan²Ф)+8tanФ]\(1-3tan²Ф)

(latex)
`(tan\theta(1-3tan^2\theta)+8\theta)/(1-3tan^2\theta)`

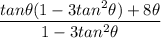
Distribute: (tan Ф - 3tan³Ф + 8Ф)\(1 - 3 tan²Ф)

(latex)
`(tan\theta-3tan^3\theta+8\theta)/(1-3tan^2\theta)`

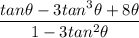
Simplify: (9Ф - 3tan³Ф)\(1 - 3 tan²Ф)

3(3Ф - tan³Ф)\(1 - 3 tan²Ф)

(latex)
`(9\theta - 3tan^3\theta)/(1-3tan^2\theta)`

`(3(3\theta - tan^3\theta))/(1-3tan^2\theta)`

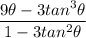
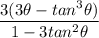
Triple Angle Identity: 3 tan 3Ф

3 tan 3Ф = 3 tan 3Ф
`\checkmark`