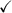Answer: see proof below
Explanation:
Use the following identities & Unit Circle calculations:
4cos³x = 3cos x + cos 3x
--> cos³x = (1/4)[3cos x + cos 3x]
4sin³x = 3sin x - sin 3x
--> sin³x = (1/4)[3sin x - sin 3x]
cos 60° = sin 30° = (1/2)
Proof: LHS → RHS
Given: cos³ 20° + sin³ 10°
Triple Angle Identity: (1/4)[3cos 20° + cos 3·20°] + (1/4)[3sin 10° - sin 3·10°]
Simplify: (1/4)[3cos 20° + cos 60° + 3sin 10° - sin 30°]
(1/4)[3cos 20° + (1/2) + 3sin 10° - (1/2)]
(1/4)[3cos 20° + 3sin 10°]
Factor: (3/4)[cos 20° + sin 10°]
Proven: (3/4)[cos 20° + sin 10°] = (3/4)[cos 20° + sin 10°]