Explanation:
Given:
- Length of the Rectangle is 3 more than its width.
- Perimeter of rectangle is 54 m
To Find:
- Length and Breadth
- Area of the rectangle
Solution:
We are given length of a rectangle is 3 more than its width
Let's assume:
- Breadth of the rectangle = x
- Length of the rectangle = x + 3
We know that,

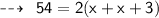
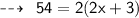
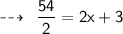
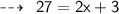

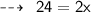


Hence,
- Breadth of rectangle = x = 12 m
- Length of rectangle = 3 + x = 15 m
Now, Finding its area:

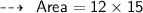
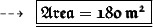
Hence,
- Length and breadth of rectangle is 12 m and 15 m
- Area of the rectangle is 180 m²