Answer:
(a) 167
(b) 7
(c) 97
Explanation:
The (1 - α)% confidence interval for the population mean μ is:
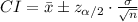
The margin of error is:
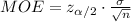
Then the formula to estimate the sample size is:
![n=[(z_(\alpha/2)\cdot \sigma )/(MOE)]^(2)](https://img.qammunity.org/2021/formulas/mathematics/college/qebac02vs4npsvmyq0e3jclkzndti63gs8.png)
(a)
For 99% confidence interval the critical value of z is:
z = 2.58.
The standard deviation is, 250.
Compute the sample size as follows:
![n=[(z_(\alpha/2)\cdot \sigma )/(MOE)]^(2)](https://img.qammunity.org/2021/formulas/mathematics/college/qebac02vs4npsvmyq0e3jclkzndti63gs8.png)
![=[(2.58* 250)/(50)]^(2)\\\\=(12.9)^(2)\\\\=166.41\\\\\approx 167](https://img.qammunity.org/2021/formulas/mathematics/college/lnn753dqsah52xpbx2p78upjys9nafe6wi.png)
The sample size that should be used is 167.
(b)
Now the standard deviation is, 50.
Compute the sample size as follows:
![n=[(z_(\alpha/2)\cdot \sigma )/(MOE)]^(2)](https://img.qammunity.org/2021/formulas/mathematics/college/qebac02vs4npsvmyq0e3jclkzndti63gs8.png)
![=[(2.58* 50)/(50)]^(2)\\\\=(2.58)^(2)\\\\=6.6564\\\\\approx 7](https://img.qammunity.org/2021/formulas/mathematics/college/bwl0gvhzl454kph2zwcil533gypxeu0s7t.png)
The sample size that should be used is 7.
(c)
Now a 95% confidence level is used.
For 95% confidence interval the critical value of z is:
z = 1.96.
Compute the sample size as follows:
![n=[(z_(\alpha/2)\cdot \sigma )/(MOE)]^(2)](https://img.qammunity.org/2021/formulas/mathematics/college/qebac02vs4npsvmyq0e3jclkzndti63gs8.png)
![=[(1.96* 250)/(50)]^(2)\\\\=(9.8)^(2)\\\\=96.04\\\\\approx 97](https://img.qammunity.org/2021/formulas/mathematics/college/3b8cmxilbqsfj6wtu8qdj0aqak906clucf.png)
The sample size that should be used is 97.