Answer:
torque to raise the load = 16.411 Nm
torque to lower the load = 8.40 Nm
overall efficiency = 0.24
Step-by-step explanation:
Given:
max load on vertical direction of the screw = Force = F = 5kN
frictional diameter of the collar = 45 mm
Diameter = 25 mm
length of pitch = 5 mm
coefficient of friction for thread µ = 0.09
coefficient of friction for collar µ
 = 0.06
= 0.06
To find:
torque to "raise" the load
torque to and "lower"
overall efficiency
Solution:
Compute torque to raise the load:
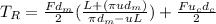
where
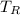 is the torque
is the torque
F is the load
 is diameter of thread
is diameter of thread
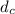 is diameter of collar
is diameter of collar
L is the thread pitch distance
µ is coefficient of friction for thread
µ
 is coefficient of friction for collar
is coefficient of friction for collar
Putting the values in above formula:
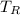 = 5(25) / 2 [5+ (π(0.09)(25) / π(25)-0.09(5)] + 5(0.06)(45) / 2
= 5(25) / 2 [5+ (π(0.09)(25) / π(25)-0.09(5)] + 5(0.06)(45) / 2
= 125/2 [5 + (3.14)(0.09)(25)/ 3.14(25)-0.45] + 13.5/2
= 62.5 [(5 + 7.065) / 78.5 - 0.45] + 6.75
= 62.5 [12.065 / 78.05 ] + 6.75
= 62.5 (0.15458) + 6.75
= 9.66125 + 6.75
= 16.41125
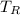 = 16.411 Nm
= 16.411 Nm
Compute torque to lower the load:
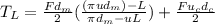
= 5(25) / 2 [ (π(0.09)(25) - L / π(25)-0.09(5) ] + 5(0.06)(45) / 2
= 125/2 [ ((3.14)(0.09)(25) - 5) / 3.14(25)-0.45 ] + 13.5/2
= 62.5 [ (7.065 - 5) / 78.5 - 0.45 ] + 6.75
= 62.5 [ 2.065 / 78.05 ] + 6.75
= 62.5 (0.026457) + 6.75
= 1.6535625 + 6.75
= 8.40 Nm
Since the torque required to lower the the load is positive indicating that an effort is applied to lower the load, Hence the thread is self locking.
Compute overall efficiency:
overall efficiency = F(L) / 2π
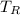
= 5(5) / 2(3.14)( 16.411)
= 25/ 103.06108
overall efficiency = 0.24