Question

Find the absolute extrema for f(x,y)=4-x^2-y^4+1/2y^2 over the closed disk D:x^2+y^2 is less than or equal to 1

Answer 1

Find the critical points of
`f(x,y)`:

`(\partial f)/(\partial x)=-2x=0\implies x=0`

`(\partial f)/(\partial y)=y-4y^3=y(1-4y^2)=0\implies y=0\text{ or }y=\pm\frac12`

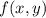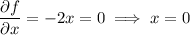
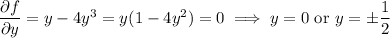
All three points lie within
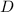`D`, and
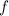`f` takes on values of

`\begin{cases}f(0,0)=4\\f\left(0,-\frac12\right)=(65)/(16)\\f\left(0,\frac12\right)=(65)/(16)\end{cases}`

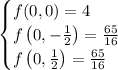
Now check for extrema on the boundary of
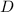`D`. Convert to polar coordinates:

`f(x,y)=f(\cos t,\sin t)=g(t)=4-\cos^2-\sin^4t+\frac12\sin^2t=3+\frac32\sin^2t-\sin^4t`

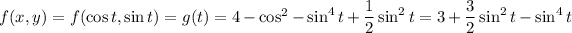
Find the critical points of
`g(t)`:

`(\mathrm dg)/(\mathrm dt)=3\sin t\cos t-4\sin^3t\cos t=\sin t\cos t(3-4\sin^2t)=0`

`\implies\sin t=0\text{ or }\cos t=0\text{ or }\sin t=\pm\frac{\sqrt3}2`

`\implies t=n\pi\text{ or }t=\frac{(2n+1)\pi}2\text{ or }\pm\frac\pi3+2n\pi`

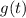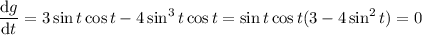
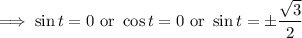
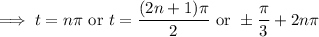
where
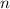`n` is any integer. There are some redundant critical points, so we'll just consider
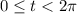`0\le t< 2\pi`, which gives

`t=0\text{ or }t=\frac\pi3\text{ or }t=\frac\pi2\text{ or }t=\pi\text{ or }t=\frac{3\pi}2\text{ or }t=\frac{5\pi}3`

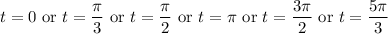
which gives values of

`\begin{cases}g(0)=3\\g\left(\frac\pi3\right)=(57)/(16)\\g\left(\frac\pi2\right)=\frac72\\g(\pi)=3\\g\left(\frac{3\pi}2\right)=\frac72\\g\left(\frac{5\pi}3\right)=(57)/(16)\end{cases}`

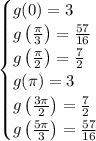
So altogether,
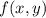`f(x,y)` has an absolute maximum of 65/16 at the points (0, -1/2) and (0, 1/2), and an absolute minimum of 3 at (-1, 0).