Question

A proposed mechanism for the reaction: 2 H2 + 2NO - N2 + 2H30 Step 1: H2g) + 2NO () - N2O (g) + H20) (slow) Step 2: N20cm) + H2 (g) - N2 (g) + H2O) (fast) What is the rate law and the intermediate respectively

Answer 1

`\text{Rate} = k\, [\mathrm{H_2\, (g)}]\cdot [\mathrm{NO\, (g)}]^2`.

`\rm N_2O\, (g)` is the intermediate.

Step-by-step explanation:

Rate

Balanced overall reaction:
`\rm 2\, H_2\, (g) + 2\, NO\, (g) \to N_2\, (g) + 2\, H_2O\, (g)`.

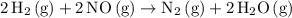Proposed mechanism:

• 
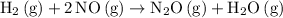  `\rm H_2\, (g) + 2\, NO\, (g) \to N_2O\, (g) + H_2O \, (g)` (slow.)
• 
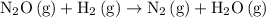  `\rm N_2O\, (g) + H_2\, (g) \to N_2\, (g) + H_2O\, (g)` (fast.)

Start with the slowest, rate-determining step of the proposed mechanism. Here, the rate-determining step is
`\rm H_2\, (g) + 2\, NO\, (g) \to N_2O\, (g) + H_2O \, (g)`.

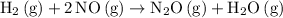There are two species on the reactant side of this intermediate reaction:
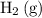`\rm H_2\, (g)` and
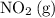`\rm NO_2\, (g)`. The concentration of both of them should be in the rate expression of this step.

On the other hand, the coefficient of
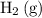`\rm H_2\, (g)` is one while the coefficient of
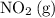`\rm NO_2\, (g)` is two. Therefore, in the rate expression of this step, the concentration of
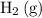`\rm H_2\, (g)\!` should have a power of one, while the concentration of
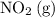`\rm NO_2\, (g)\!` should have a power of two.

include the rate constant
`k` to obtain the rate expression of the rate-determining slow step:

`\text{Rate} = k\, [\mathrm{H_2\,(g)}]\cdot [\mathrm{NO\, (g)}]^2`.

Make sure that all species in this rate expression are on the reactant side of the overall balanced reaction. Otherwise, further steps would be required to obtain the rate law of the overall reaction.

Therefore, by this proposed mechanism, the rate law of the overall reaction would be
`\text{Rate} = k\, [\mathrm{H_2\,(g)}]\cdot [\mathrm{NO\, (g)}]^2`.

Intermediate

In a proposed reaction mechanism, a species is an intermediate if it appeared in one of the proposed steps, but not in the balanced overall equation.

The two steps of this proposed mechanism mentioned five species:

• 
  `\rm H_2\, (g)`.
• 
  `\rm NO\,(g)`.
• 
  `\rm N_2O\, (g)`.
• 
  `\rm H_2O\, (g)`.
• 
  `\rm N_2\, (g)`.

With the exception of
`\rm N_2O\, (g)`, all the other species appeared in the overall balanced equation. Therefore,
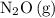`\rm N_2O\, (g)\!` is the intermediate.