Question

What is the smallest positive integer $n$ such that $\frac{n}{n+101}$ is equal to a terminating decimal?

Answer 1

n = 24

Explanation:

Given the fraction:

`$(n)/(n+101)$`

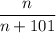
To find:

Smallest positive integer
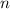`$n$` such that the fraction is equal to a terminating decimal.

Solution:

The rule that a fraction is equal to a terminating decimal states that, the denominator must contain factors of only 2 and 5.

i.e. Denominator must look like
`2^m* 5^n`, only then the fraction will be equal to a terminating decimal.

Now, let us have a look at the denominator,
`n+101`

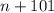
Let us use hit and trial method to find the value of
`n` as positive integer.

n = 1, denominator becomes 102 =
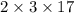`2 * 3 * 17` not of the form
`2^m* 5^n`.

n = 4, denominator becomes 105 =
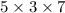`5 * 3 * 7` not of the form
`2^m* 5^n`.

n = 9, denominator becomes 110 =
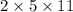`2 * 5 * 11` not of the form
`2^m* 5^n`.

n = 14, denominator becomes 115 =
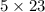`5 * 23` not of the form
`2^m* 5^n`.

n = 19, denominator becomes 120 =
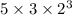`5 * 3 * 2^3` not of the form
`2^m* 5^n`.

n = 24, denominator becomes 125 =
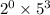`2^0 * 5 ^3` It is of the form
`2^m* 5^n`.

So, the answer is n = 24