Question

The lengths of pregnancies in a small rural village are normally distributed with a mean of 265 days and a standard deviation of 14 days. In what range would we expect to find the middle 50% of most lengths of pregnancies

Answer 1

the middle 50% of most lengths of pregnancies ranges between 255.62 days and 274.38 days

Explanation:

Given that :

Mean = 265

standard deviation = 14

The formula for calculating the z score is
`z = (x -\mu)/(\sigma)`

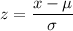
x = μ + σz

At middle of 50% i.e 0.50

The critical value for
`z_(\alpha/2) = z_(0.50/2)`

From standard normal table

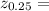`z_(0.25)=` + 0.67 or -0.67

So; when z = -0.67

x = μ + σz

x = 265 + 14(-0.67)

x = 265 -9.38

x = 255.62

when z = +0.67

x = μ + σz

x = 265 + 14 (0.67)

x = 265 + 9.38

x = 274.38

the middle 50% of most lengths of pregnancies ranges between 255.62 days and 274.38 days