Question

Salaries of 42 college graduates who took a statistics course in college have a​ mean, ​, of . Assuming a standard​ deviation, ​, of ​$​, construct a ​% confidence interval for estimating the population mean .

Answer 1

The 99% confidence interval for estimating the population mean μ is ($60,112.60, $68087.40).

Explanation:

The complete question is:

Salaries of 42 college graduates who took a statistics course in college have a​ mean,
`\bar x` of, $64, 100. Assuming a standard​ deviation, σ of ​$10​,016 construct a ​99% confidence interval for estimating the population mean μ.

Solution:

The (1 - α)% confidence interval for estimating the population mean μ is:

`CI=\bar x\pm z_(\alpha/2)(\sigma)/(√(n))`

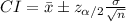
The critical value of z for 99% confidence interval is:

`z_(\alpha/2)=z_(0.01/2)=z_(0.005)=2.57`

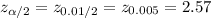
Compute the 99% confidence interval for estimating the population mean μ as follows:

`CI=\bar x\pm z_(\alpha/2)(\sigma)/(√(n))`

`=64100\pm 2.58*(10016)/(√(42))\\\\=64100+3987.3961\\\\=(60112.6039, 68087.3961)\\\\\approx (60112.60, 68087.40)`

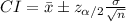
Thus, the 99% confidence interval for estimating the population mean μ is ($60,112.60, $68087.40).