Answer:
The 99% confidence interval for estimating the population mean μ is ($60,112.60, $68087.40).
Explanation:
The complete question is:
Salaries of 42 college graduates who took a statistics course in college have a mean,
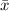 of, $64, 100. Assuming a standard deviation, σ of $10,016 construct a 99% confidence interval for estimating the population mean μ.
of, $64, 100. Assuming a standard deviation, σ of $10,016 construct a 99% confidence interval for estimating the population mean μ.
Solution:
The (1 - α)% confidence interval for estimating the population mean μ is:
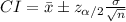
The critical value of z for 99% confidence interval is:
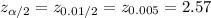
Compute the 99% confidence interval for estimating the population mean μ as follows:
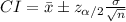

Thus, the 99% confidence interval for estimating the population mean μ is ($60,112.60, $68087.40).