Answer:
circumference of the satellite orbit = 4.13 × 10⁷ m
Step-by-step explanation:
Given that:
the time period T = 88.5 min = 88.5 × 60 = 5310 sec
The mass of the earth
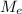 = 5.98 × 10²⁴ kg
= 5.98 × 10²⁴ kg
if the radius of orbit is r,
Then,
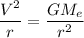
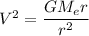
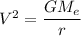
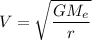
Similarly :
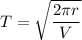
where;
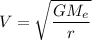
Then:
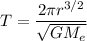
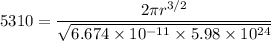
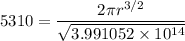
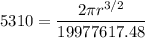
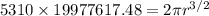
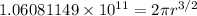
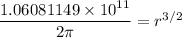
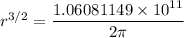
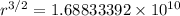
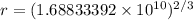
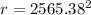
r = 6579225 m
The circumference of the satellites orbit can now be determined by using the formula:
circumference = 2π r
circumference = 2π × 6579225 m
circumference = 41338489.85 m
circumference of the satellite orbit = 4.13 × 10⁷ m