Question

At what speed (in m/s) will a proton move in a circular path of the same radius as an electron that travels at 7.45 ✕ 106 m/s perpendicular to the Earth's magnetic field at an altitude where the field strength is 1.10 ✕ 10−5 T

Answer 1

The speed of the proton is 4059.39 m/s

Step-by-step explanation:

The centripetal force on the particle is given by;

`F = (mv^2)/(r)`

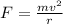
The magnetic force on the particle is given by;

`F = qvB`

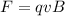
The centripetal force on the particle must equal the magnetic force on the particle, for the particle to remain in the circular path.

`(mv^2)/(r) = qvB\\\\r = (mv^2)/(qvB) \\\\r = (mv)/(qB)`

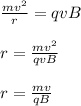
where;

r is the radius of the circular path moved by both electron and proton;

⇒For electron;

`r = ((9.1*10^(-31))(7.45*10^6))/((1.602*10^(-19))(1.1*10^(-5)))\\\\r = 3.847 \ m`

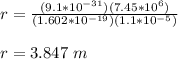
⇒For proton

The speed of the proton is given by;

`r = (mv)/(qB)\\\\mv = qBr\\\\v = (qBr)/(m) \\\\v = ((1.602*10^(-19))(1.1*10^(-5))(3.847))/(1.67*10^(-27)) \\\\v = 4059.39 \ m/s`

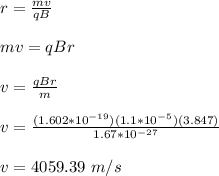
Therefore, the speed of the proton is 4059.39 m/s