Question

Which of the following functions has a vertical asymptote at x = 2, a horizontal

asymptote at f(x) = 1, and a root at x = -1?
A.f(x) = 2 + 1
B.f(x) = x 2 + 1
c.f(x) = x 2 - 1
D.f(x) == +1

Answer 1

The function with a vertical asymptote at x = 2, a horizontal asymptote at f(x) = 1, and a root at x = -1 is C. f(x) = x^2 - 1.

Step-by-step explanation:

To determine which function has a vertical asymptote at x = 2, a horizontal asymptote at f(x) = 1, and a root at x = -1, we need to analyze the equations. Let's evaluate each option:

1. f(x) = 2 + 1: This function is a constant function and does not have any asymptotes or roots.
2. f(x) = x2 + 1: This function has a vertex at (0, 1), no vertical asymptote at x = 2, and no root at x = -1.
3. f(x) = x2 - 1: This function has a vertical asymptote at x = 2, a horizontal asymptote at f(x) = 1, and a root at x = -1.
4. f(x) = +1: This constant function does not have any asymptotes or roots.

Therefore, the correct answer is c.f(x) = x 2 - 1

Answer 2

First, an asymptote means that the function "tends to go" to a value, bt actually never reaches it.

The functions here are:

A.f(x) = 2 + 1

B.f(x) = x^2 + 1

c.f(x) = x^2 - 1

D.f(x) == +1

The functions are really poorly written, but i will try to answer this.

first:

"a root at x = -1"

Means that f(-1) = 0,

The only function that is zero when x = -1, is the option c.

f(-1) = (-1)^2 - 1 = 1 - 1 = 0.

Now, if we want to have a vertical asymptote at x = 2, then we should have a function like:

`f(x) = (something)/(x - 2)`

So we want to have a quotient, where the denominator is equal to zero when x = 2, this will lead to a vertical asymptote.

I can not see this in the options provided, so i guess that the functions are just not well written.

For a horizontal asymptote, we have something like:

`f(x) = (something)/(x) + 1`

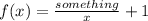
So as x starts to grow, the first term in the function will start to decrease, until it becomes really close to zero (but is never equal to zero) so in that case we have an horizontal asymptote to f(x) = 1.