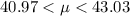Question

The time it takes to install a certain hardware is random. A technician installs this hardware on 64 computers with the average installation time being 42 minutes and the standard deviation of the times being 5 minutes. What is a 90% confidence interval for the popu

Answer 1

`40.97<\mu<43.03`

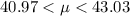
Explanation:

Th formula for calculating the confidence interval of a population is expressed as shown;

CI = xbar ± Z*S/√n where;

xbar is the mean or average sample

Z is the z-score at 90% confidence

S is the standard deviation

n is the sample size

Given parameters

xbar = 42

Z at 90% CI = 1.645

S = 5

n = 64

Substituting the values into the formula will give;

CI = 42±(1.645*5/√64)

CI = 42±(1.645*5/8)

CI = 42±(1.645*0.625)

CI = 42±1.028125

CI = (42-1.028125, 42+1.028125)

CI = (40.971875, 43.028125)

Hence the 90% confidence interval for the population is approximately (40.97, 43.03) i.e
`40.97<\mu<43.03`