Answer:
El móvil B necesita 60 segundos para alcanzar al móvil A y le alcanza una distancia de 2400 metros con respecto al punto de referencia.
Explanation:
Supóngase que cada movil viaja en el mismo plano y que el móvil B se localiza inicialmente en la posición
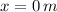 , mientras que el móvil A se encuentra en la posición
, mientras que el móvil A se encuentra en la posición
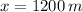 . Ambos móviles viajan a rapidez constante. Si el móvil B alcanza al móvil A después de cierto tiempo, el sistema de ecuaciones cinemáticas es el siguiente:
. Ambos móviles viajan a rapidez constante. Si el móvil B alcanza al móvil A después de cierto tiempo, el sistema de ecuaciones cinemáticas es el siguiente:
Móvil A
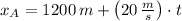
Móvil B
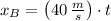
Donde:
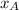 ,
,
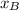 - Posiciones finales de cada móvil, medidas en metros.
- Posiciones finales de cada móvil, medidas en metros.
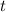 - Tiempo, medido en segundos.
- Tiempo, medido en segundos.
Si
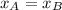 , el tiempo requerido por el móvil B para alcanzar al móvil A es:
, el tiempo requerido por el móvil B para alcanzar al móvil A es:
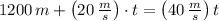
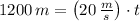
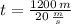
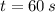
El móvil B necesita 60 segundos para alcanzar al móvil A.
Ahora, la distancia se obtiene por sustitución directa en cualquiera de las ecuaciones cinemáticas:
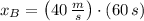
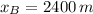
El móvil B alcanza al móvil A a una distancia de 2400 metros con respecto al punto de referencia.