Question

The position of an object at time t is given by s(t) = -9 - 3t. Find the instantaneous velocity at t = 8 by finding the derivative. I think its either -3 or -36

Answer 1

`\boxed{\sf Instantaneous \ velocity \ (v) = -3}`

Given:

Relation between position of an object at time t is given by:

s(t) = -9 - 3t

To Find:

Instantaneous velocity (v) at t = 8

Explanation:

To find instantaneous velocity we will differentiate relation between position of an object at time t by t:

`\sf \implies v = (d)/(dt) (s(t))`

`\sf \implies v = (d)/(dt) ( - 9 - 3t)`

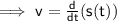
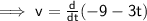
Differentiate the sum term by term and factor out constants:

`\sf \implies v = (d)/(dt) ( - 9) - 3 ((d)/(dt) (t))`

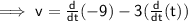
The derivative of -9 is zero:

`\sf \implies v = - 3( (d)/(dt) (t)) + 0`

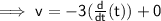
Simplify the expression:

`\sf \implies v = - 3( (d)/(dt) (t))`

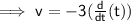
The derivative of t is 1:

`\sf \implies v = - 3 * 1`

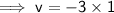
Simplify the expression:

`\sf \implies v = - 3`

(As, there is no variable after differentiating the relation between position of an object at time t by t so at time t = 8 is of no use.)

So,

Instantaneous velocity (v) at t = 8 is -3