Complete Question
Two samples from the same population both have M = 84 and s2 = 20, but one sample has n = 10 and the other has n = 20 scores. Both samples are used to evaluate a hypothesis stating that μ = 80 and to compute Cohen’s d. How will the outcomes for the two samples compare?
a.
The larger sample is more likely to reject the hypothesis and will produce a larger value for Cohen’s d.
b.
The larger sample is more likely to reject the hypothesis, but the two samples will have the same value for Cohen’s d.
c.
The larger sample is less likely to reject the hypothesis and will produce a larger value for Cohen’s d.
d.
The larger sample is less likely to reject the hypothesis, but the two samples will have the same value for Cohen’s d.
Answer:
The Cohen's d value is
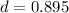
The correct option is b
Explanation:
From the question we are told that
The sample mean of each population is
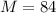
The variance of each population is
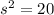
The first sample size is
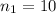
The second sample size is
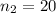
The null hypothesis is

Generally the standard deviation is mathematically evaluated as

=>
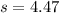
The first test statistics is evaluated as
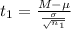
=>

=>

The second test statistics is evaluated as
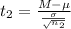
=>
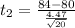
=>

The sample with the larger test statistics (sample size) will more likely reject the null hypothesis
Generally the Cohen's d value is mathematically evaluated as
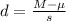
=>
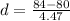
=>
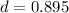
Given that the the sample mean and sample size are the same for both sample the Cohen's d value will be the same