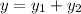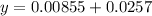Question

A 2-slit arrangement with 60.3 μm separation between the slits is illuminated with 482.0 nm light. Assuming that a viewing screen is located 2.14 m from the slits, find the distance from the first dark fringe on one side of the central maximum to the second dark fringe on the other side. A. 24.1 mm B. 34.2 mm C. 68.4 mm D. 51.3 mm

Answer 1

The distance is
`y = 0.03425 \ m`

Step-by-step explanation:

From the question we are told that

The distance of separation is
`d = 60.3 \mu m= 60.3 *10^(-6)\ m`

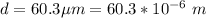
The wavelength is
`\lambda = 482.0 \ nm = 482.0 *10^(-9) \ m`

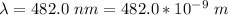
The distance of the screen is
`D = 2.14 \ m`

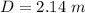
Generally the distance of a fringe from the central maxima is mathematically represented as

`y = [m + (1)/(2) ] * (\lambda * D)/(d)`

For the first dark fringe m = 0

`y_1 = [0 + (1)/(2) ] * (482*10^(-9) * 2.14)/( 60.3*10^(-6))`

`y_1 = 0.00855 \ m`

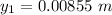
For the second dark fringe m = 1

`y_2 = [1 + (1)/(2) ] * (482*10^(-9) * 2.14)/( 60.3*10^(-6))`

`y_2 = 0.0257 \ m`

So the distance from the first dark fringe on one side of the central maximum to the second dark fringe on the other side is

`y = y_1 + y_2`

`y = 0.00855 + 0.0257`

`y = 0.03425 \ m`