Answer:
the company should not buy the machine.
Step-by-step explanation:
Given that:
cost of the new machine = $38000
lifespan = 8 years
constant income = 5,000
Interest = 1.7%
no of days = 365
The value of earning at the time of buying can be calculated as follows:
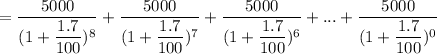
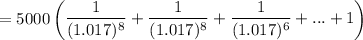
Sum of a Geometric progression
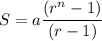
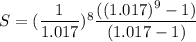
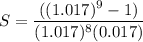
S = 8.4211
The value of earning at the time of buying = (5000 × 8.4211)-$5000
The value of earning at the time of buying = $42105.5 -$5000
The value of earning at the time of buying = $37105.5
The Machine price = $38000
If the value - Machine price > 0, then the company should buy the machine
∴
= $ 37105.5 - $38000
= -$ 894.5
Since the value is negative which is less than zero, then the company should not buy the machine.