Question

What is the equation of the line that passes through the point (2, -1) and has a

slope of
3/2

Answer 1

y= 3/2x -4

Explanation:

Since we are given a point and a slope, we can use the point-slope formula.

`y-y_(1) = m(x-x_(1))`

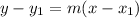
where m is the slope and (x1, y1) is a point the line passes through.

We know the slope is 3/2 and the point we are given is (2, -1).

`m=(3)/(2) \\\\x_(1) = 2\\\\y_(1) = -1`

Substitute the values into the formula.

`y- -1 = (3)/(2) (x-2)`

`y+1=(3)/(2) (x-2)`

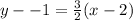
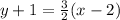
We want to find the equation of line , which is y=mx+b ( m is the slope and b is the y-intercept). Therefore, we must get y by itself on the left side of the equation.

First, distribute the 3/2. Multiply each term inside the parentheses by 3/2.

`y+1= ((3)/(2) * x) + ((3)/(2) *-2)`

`y+1= (3)/(2)x + ((3)/(2) *-2)`

`y+1=(3)/(2) x + -3`

`y+1=(3)/(2) x -3`

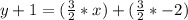
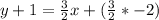
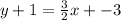
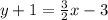
Next, subtract 1 from both sides.

`y+1-1=(3)/(2) x + -3 -1`

`y=(3)/(2) x + -3 -1`

`y=(3)/(2) x -4`

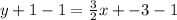
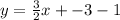
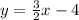
Now the line is in slope intercept form, therefore the equation of the line is y=3/2x -4. The slope of the line is 3/2 and the y-intercept is -4.

Answer 2

The answer is

`y = (3)/(2) x - 4`

Explanation:

To find the equation of the line using a point and slope we use the formula

y - y1 = m(x - x1)

where m is the slope

(x1 ,y1) is the given point

From the question

slope = 3/2

point = ( 2 , - 1)

Substitute these values into the above formula

That's

`y + 1 = (3)/(2) (x - 2)`

`y + 1 = (3)/(2) x - 3`

`y = (3)/(2) x - 3 - 1`

We have the final answer as

`y = (3)/(2) x - 4`

Hope this helps you