Question

The radius of the circle is increasing at a rate of 1 meter per day and the sides of the square are increasing at a rate of 3 meters per day. When the radius is 3 meters, and the sides are 20 meters, then how fast is the AREA outside the circle but inside the square changing

Answer 1

The area inside the square and outside the circle is changing at a rate of 101.150 square meters per day.

Explanation:

According to the statement of the problem, the circle is inside the square and the area inside the square but outside the circle, measured in square meters, is represented by the following formula. It is worth to notice that radius (
`r`) is less than side (
`l`), both measured in meters:

`A_(T) = A_(\square) -A_(\circ)`

`A_(T) = l^(2)-\pi\cdot r^(2)`

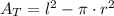
Now, the rate of change of the total area is calculated after deriving previous expression in time:

`(dA_(T))/(dt) = 2\cdot l\cdot (dl)/(dt) -2\pi\cdot r\cdot (dr)/(dt)`

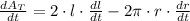
Where
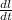`(dl)/(dt)` and
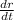`(dr)/(dt)` are the rates of change of side and radius, measured in meters per day.

Given that
`l = 20\,m`,
`r = 3\,m`,
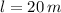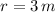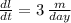`(dl)/(dt) = 3\,(m)/(day)` and
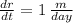`(dr)/(dt) = 1\,(m)/(day)`, the rate of change of the total area is:

`(dA_(T))/(dt) = 2\cdot (20\,m)\cdot \left(3\,(m)/(day) \right)-2\pi\cdot (3\,m)\cdot \left(1\,(m)/(day) \right)`

`(dA_(T))/(dt) \approx 101.150\,(m^(2))/(day)`

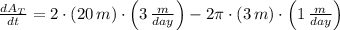
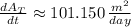
The area inside the square and outside the circle is changing at a rate of 101.150 square meters per day.