Question

Suppose 232subjects are treated with a drug that is used to treat pain and 50of them developed nausea. Use a 0.01significance level to test the claim that more than 20​%of users develop nausea. Identify the null and alternative hypotheses for this test.

A. Upper H0?: p equals 0.20
Upper H1?: p not equals 0.20
B. Upper H0?: p equals 0.20
Upper H1?: p greater than 0.20
C. Upper H0?: p greater than 0.20
Upper H1?: p equals 0.20
D. Upper H0?: p equals 0.20
Upper H1?: p less than 0.20
Identify the test statistic for this hypothesis test. Identify the​ P-value for this hypothesis test.
Identify the conclusion for this hypothesis test.
A. Reject Upper H 0. There is sufficient evidence to warrant support of the claim that more than 20?% of users develop nausea.
B. Fail to reject Upper H 0. There is sufficient evidence to warrant support of the claim that more than 20?% of users develop nausea.
C. Reject Upper H 0. There is not sufficient evidence to warrant support of the claim that more than 20?% of users develop nausea.
D. Fail to reject Upper H 0. There is not sufficient evidence to warrant support of the claim that more than 20?% of users develop nausea.

Answer 1

A

The correct option is B

B

`t = 0.6093`

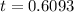
C

`p-value = 0.27116`

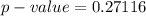
D

The correct option is D

Explanation:

From the question we are told that

The sample size is
`n = 232`

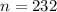
The number that developed nausea is X = 50

The population proportion is p = 0.20

The null hypothesis is
`H_o : p = 0.20`

The alternative hypothesis is
`H_a : p > 0.20`

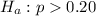
Generally the sample proportion is mathematically represented as

`\r p = (50)/(232)`

`\r p = 0.216`

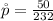
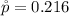
Generally the test statistics is mathematically represented as

=>
`t = \frac{\r p - p }{ \sqrt{ (p(1- p ))/(n) } }`

=>
`t = \frac{ 0.216 - 0.20 }{ \sqrt{ ( 0.20 (1- 0.20 ))/( 232) } }`

=>
`t = 0.6093`

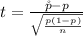
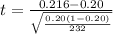
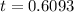
The p-value obtained from the z-table is

`p-value = P(Z > 0.6093) = 0.27116`

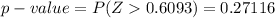
Given that the
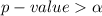`p-value > \alpha` then we fail to reject the null hypothesis