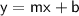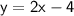Question

85 POINTS! PLEASE HELP! Explain how to write an equation parallel to the equation y = 2x + 3 and the new line also includes the ordered pair (1,-2).

Answer 1

y = 2x - 4

Explanation:

the problem is called (slope-intercept form)

the equation of the line is y = mx + b

the equation of a line is given as y = 2x + 3

slope = 2

b = y-intercept is where the line crosses the y-axis = 3

so point (x1, y1) = (1, -2)

by using the equation.

y = mx + b

-2 = 2 (1) + b

-2 -2 = b

therefore b = -4

writing the new equation using the slope intercept form

y = mx + b would be y = 2x + 4

so the equation parallel to the equation y = 2x + 3 is y = 2x - 4

Answer 2

`\huge\boxed{\sf y = 2x -4}`

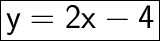
Explanation:

The given equation is:

y = 2x + 3

Where Slope = m = 2 , Y-intercept = b = 3

Parallel lines have equal slopes

So, Slope of new line = m = 2

Now, Finding y-intercept:

Given Point = (x,y) = (1,-2)

So, x = 1 , y = -2

Putting m, x and y in standard form of equation to get b:

`\sf y = mx+b`

`\sf -2 = (2)(1) + b\\-2 = 2 + b\\`

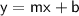
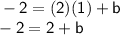
Subtracting 2 to both sides

`\sf b = -2-2\\`

b = -4

So, the standard form og equation for the new line is :

`\sf y = mx+b`

`\sf y = 2x -4`