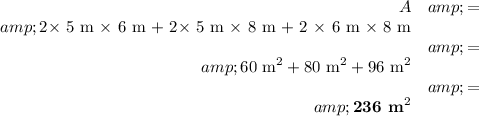Answer:
Here's what I get
Explanation:
a. Net of a cube
Fig. 1 is the net of a cube
b. Does the formula work?
Tony's formula works if you ignore dimensions.
There are six squares in the net of a cube.
If each side has a unit length s, the total area of the cube is 6s.
c. Will the formula work for any rectangular prism?
No, because a rectangular prism has sides of three different lengths — l, w, and h — as in Fig. 2.
d. Area of a rectangular prism
A rectangular prism has six faces.
A top (T) and a bottom (b) — A = 2×l×w
A left (L) and a right (R) — A = 2×l×h
A front (F) and a back (B) — A = 2×w×h
Total area = 2lw + 2lh + 2wh
If l = 5 m, w = 6 m and h = 8 m,