Question

Rectangular cube 3.2 m length 1.2 m in height and 5 m in length is split into two parts. The container has a movable airtight divider that divides its length as necessary. Part A has 58 moles of gas and part B has 165 moles of a gas.

Required:
At what length will the divider to equilibrium?

Answer 1

The length the divider is to equilibrium from Part A = 1.30 m and from Part B = 3.70 m

Step-by-step explanation:

Given that:

A rectangular cube with 3.2 m breadth, 1.2 m height and 5 m in length is splitted into two parts.

The diagrammatic expression for the above statement can be found in the attached diagram below.

The container has a movable airtight divider that divides its length as necessary.

Part A has 58 moles of gas

Part B has 165 moles of a gas.

Thus, the movable airtight divider will stop at a length where the pressure on it is equal on both sides.

i.e

`\mathtt{P = P_A = P_B}`

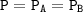
Using the ideal gas equation,

PV = nRT

where, P,R,and T are constant.

Then :

`\mathsf{(V_A)/(n_A)= (V_B)/(n_B)}`

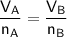
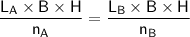`\mathsf{(L_A * B * H)/(n_A)= (L_B * B * H)/(n_B)}` --- (1)

since Volume of a cube = L × B × H

From the question; the L = 5m

i,e

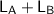`\mathsf{L_A +L_B}` = 5

`\mathsf{L_A = 5 - L_B}`

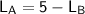
From equation (1) , we divide both sides by (B × H)

Then :

`\mathsf{(L_A )/(n_A)= (L_B )/(n_B)}`

`\mathsf{(5-L_B)/(58)= (L_B )/(165)}`

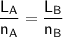
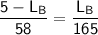
By cross multiplying; we have:

165 ( 5 -
`\mathsf{L_B}` ) = 58 (

825 - 165
`\mathsf{L_B}` = 58

825 = 165
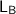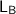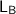`\mathsf{L_B}` +58

825 = 223
`\mathsf{L_B}`

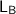
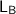`\mathsf{L_B}` = 825/223

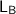`\mathsf{L_B}` = 3.70 m

`\mathsf{L_A = 5 - L_B}`

`\mathsf{L_A = 5 - 3.70}`

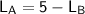
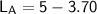
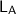`\mathsf{ L_A}` = 1.30 m

The length the divider is to equilibrium from Part A = 1.30 m and from Part B = 3.70 m