Question

You have a lightweight spring whose unstretched length is 4.0 cm. First, you attach one end of the spring to the ceiling and hang a 1.8 g mass from it. This stretches the spring to a length of 5.2 cm . You then attach two small plastic beads to the opposite ends of the spring, lay the spring on a frictionless table, and give each plastic bead the same charge. This stretches the spring to a length of 4.8 cm .

Required:
What is the magnitude of the charge (in nC) on each bead?

Answer 1

To find the magnitude of the charge of each plastic bead, we can use Coulomb's Law and the concept of electrical potential energy. By calculating the change in potential energy and equating it to the work done by the spring force, we can determine that each plastic bead has a charge of approximately 5.7 nC.

Step-by-step explanation:

To determine the magnitude of the charge on each plastic bead, we need to use Coulomb's Law and the concept of electrical potential energy. Starting with the given information, the spring stretches from 4.0 cm to 5.2 cm when a 1.8 g mass is attached to it and from 4.0 cm to 4.8 cm when the plastic beads are charged.

Using these values, we can calculate the change in potential energy for each scenario and equate it to the work done by the spring force, which is equal to the force constant times the displacement. By solving these equations, we can find the charge on each plastic bead to be approximately 5.7 nC.

Answer 2

The magnitude of the charge is 54.9 nC.

Step-by-step explanation:

The charge on each bead can be found using Coulomb's law:

`F_(e) = (k*q_(1)q_(2))/(r^(2))`

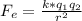
Where:

q₁ and q₂ are the charges, q₁ = q₂

r: is the distance of spring stretching = 4.8x10⁻² m

`F_(e)`: is the electrostatic force

`F_(e) = (k*q^(2))/(r^(2)) \rightarrow q = \sqrt{(F_(e))/(k)}*r`

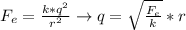
Now, we need to find
`F_(e)`. To do that we have that Fe is equal to the spring force (
`F_(k)`):

`F_(e) = F_(k) = -kx`

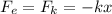
Where:

k is the spring constant

x is the distance of the spring = 4.8 - 4.0 = 0.8 cm

The spring constant can be found by equaling the sping force and the weight force:

`F_(k) = -W`

`-k*x = -m*g`

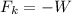
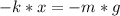
where x is 5.2 - 4.0 = 1.2 cm, m = 1.8 g and g = 9.81 m/s²

`k = (mg)/(x) = (1.8 \cdot 10^(-3) kg*9.81 m/s^(2))/(1.2 \cdot 10^(-2) m) = 1.47 N/m`

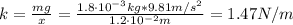
Now, we can find the electrostatic force:

`F_(e) = F_(k) = -kx = -1.47 N/m*0.8 \cdot 10^(-2) m = -0.0118 N`

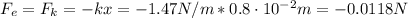
And with the magnitude of the electrostatic force we can find the charge:

`q = \sqrt{(F_(e))/(k)}*r = \sqrt{(0.0118 N)/(9 \cdot 10^(9) Nm^(2)/C^(2))}*4.8 \cdot 10^(-2) m = 54.9 \cdot 10^(-9) C = 54.9 nC`

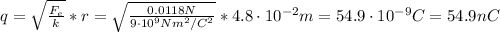
Therefore, the magnitude of the charge is 54.9 nC.

I hope it helps you!