Question

A 0.100-kg metal rod carrying a current of 15.0 A glides on two horizontal rails 0.550 m apart and 2.0 m long,

(a) If the coefficient of kinetic friction between the rod and rails is 0.120, what vertical magnetic field is required to keep the rod moving at a constant speed?
(b) If the friction between the rod and rail is reduced zero, the rod will accelerate. If the rod starts from rest at the one end of the rails, what is the speed of the rod at the other end of the rails for this frictionless situation? Use the same field value you calculated in part (a).

Answer 1

The speed of the rod is 2.169 m/s.

Step-by-step explanation:

Given that,

Mass = 0.100 kg

Current = 15.0 A

Distance = 2 m

Length = 0.550 m

Kinetic friction = 0.120

(a). We need to calculate the magnetic field

Using relation of frictional force and magnetic force

`F_(f)=F_(B)`

`\mu mg=Bli`

`B=(\mu mg)/(li)`

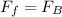
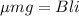
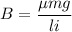
Where, l = length

i = current

m = mass

Put the value into the formula

`B=(0.120*0.1*9.8)/(0.550*15.0)`

`B=0.01425\ T`

`B=1.425*10^(-2)\ T`

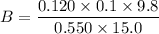
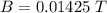
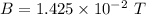
(b). If the friction between the rod and rail is reduced zero.

So,
`f_(f)=0`

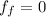
We need to calculate the acceleration

Using formula of force

`F_(net)=f_(f)+F_(B)`

`F_(net)=0+Bil`

`ma=Bil`

`a=(Bil)/(m)`

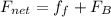
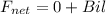
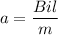
Put the value into the formula

`a=(1.425*10^(-2)*15*0.55)/(0.1)`

`a=1.176\ m/s^2`

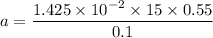
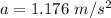
We need to calculate the speed of the rod

Using equation of motion

`v^2=u^2+2as`

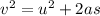
Put the value into the formula

`v^2=0+2*1.176*2`

`v^2=√(4.704)\ m/s`

`v=2.169\ m/s`

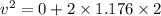
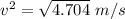
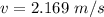
Hence, The speed of the rod is 2.169 m/s.