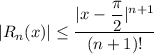Answer:
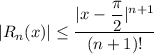
Explanation:
From the given question; the objective is to show that :
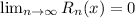 for all x in the interval of convergence f(x)=cos x, a= π/2
for all x in the interval of convergence f(x)=cos x, a= π/2
Assuming for the convergence f the taylor's series , f happens to be the derivative on an open interval I with a . Then the Taylor series for the convergence of f , for all x in I , if and only if
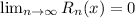
where;
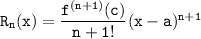
is a remainder at x and c happens to be between x and a.
Given that:
a= π/2
Then; the above equation can be written as:
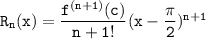
so c now happens to be the points between π/2 and x
If we recall; we know that:
 (as a result of the value of n)
(as a result of the value of n)
However, it is true that for all cases that
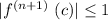
Hence, the remainder terms is :
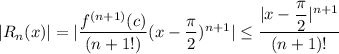
If
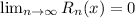 for all x and x is fixed, Then
for all x and x is fixed, Then