Question

What is the equation of the line shown in this graph?

Answer 1

y = 1

Explanation:

The equation of a line is:

`\boxed{ \mathsf{y = mx + c}}`

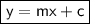
Here,

• m = slope of the line
• c = y-intercept
• y and x are variables

Finding the slope:

The slope of the line is zero, as the line is parallel to the x-axis.

Another way of finding the slope is by calculating the change in y concerning the change in x.

If we take two points that lie on the given line, like:

• (2,1)
• (-4,1)

`\boxed{slope = (1 - 1)/(2 - ( - 4)) } \\ = 0`

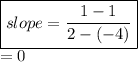
So, either way, we get the slope as zero.

=> m = 0

Finding the y-intercept:

The y-intercept of a line is the value of the y coordinate at which the line meets the y-axis, I.e.,

The point that lies on the line with its abscissa(x coordinate) zero.

Here, one such point is:

• (0, 1)

its y-intercept is 1.

=> c = 1

Finding the equation:

y = mx + c

y = 0 + 1

=> y = 1

That's the equation we've been looking for!

Answer 2

• y = 1

Explanation:

The line is parallel to the x-axis and all the points have y- coordinate of 1.

The line is:

• y = 1