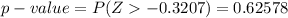Answer:
The p-value is

Explanation:
From the question we are told that
The sample size of male infant is
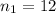
The sample size of female infant is
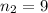
The sample mean of male infant is
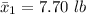
The sample mean of female infant is
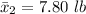
The population standard deviation is
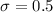
The significance level is

The null hypothesis is
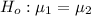
The alternative hypothesis is
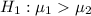
The test statistics is mathematically represented as
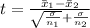
=>
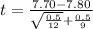
=>
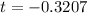
From the z-table the p-value is obtained, the value is