Question

Paul, a dentist, determined that the number of cavities that develops in his patient's mouth each year varies inversely to the number of seconds spent brushing each night. His patient, Lori, had 4 cavities when brushing her teeth 30 seconds each night. Write the equation that relates the number of cavities, c, to the time, t, spent brushing. How many cavities would Paul expect Lori to have if she had brushed her teeth for 120 seconds each night?

Answer 1

1 cavity

Explanation:

The inverse equation is x*y=k, where x is the amount of cavities, y is the time brushed, and k is a constant number. In your scenario, x is c and y is t, but you can really use any name for the variable. In the first equation 23 have 4*30=120, which is just a constant number. now that we know our constant, we can plug is into our second equation, and we get c*120=120. By dividing both sides by 120, c=1. This means that Paul will have 1 cavity.

Answer 2

Explanation:

Inverse variation is written as

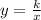`y=(k)/(x)` which, in words, says "y varies inversely with x". If cavities varies inversely with time brushing, then

`c=(k)/(t)`

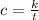
We are given the initial condition for which we need to solve for k:

c = 4 when t = 30:

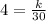`4=(k)/(30)` so

k = 120.

Now we will use that value of k to solve the problem of how many cavities, c, would she have if she brushed her teeth 120 seconds, t, each night:

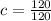`c=(120)/(120)` (the 120 on top is the k value and the 120 on the bottom is the number of seconds she brushed) to get

c = 1