Answer:
Explanation:
Inverse variation is written as
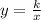 which, in words, says "y varies inversely with x". If cavities varies inversely with time brushing, then
which, in words, says "y varies inversely with x". If cavities varies inversely with time brushing, then
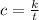
We are given the initial condition for which we need to solve for k:
c = 4 when t = 30:
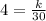 so
so
k = 120.
Now we will use that value of k to solve the problem of how many cavities, c, would she have if she brushed her teeth 120 seconds, t, each night:
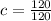 (the 120 on top is the k value and the 120 on the bottom is the number of seconds she brushed) to get
(the 120 on top is the k value and the 120 on the bottom is the number of seconds she brushed) to get
c = 1