Answer:
-10
Explanation:
Given the equation solved by savanah expressed as
 , IF she solved for one of the solution and got x = -2, we are to solve for the other value of x.
, IF she solved for one of the solution and got x = -2, we are to solve for the other value of x.
Note that the expression in modulus can be expressed as a positive expression and negative expression.
For the positive value of the expression
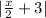 i.e
i.e
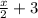 , the expression becomes;
, the expression becomes;
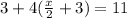
On simplification;

For the negative value of the expression
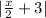 i.e
i.e
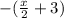 , the expression becomes;
, the expression becomes;
![3+4[-((x)/(2) + 3)] = 11](https://img.qammunity.org/2021/formulas/mathematics/college/iu6xjz507ogv9lefuy9van57qzdy4uvxm6.png)
On simplifying;
![3+4[-((x)/(2) + 3)] = 11\\\\3+4(-(x)/(2) - 3)= 11\\\\3-4((x)/(2)) -12 = 11\\\\3 - (4x)/(2) - 12 = 11\\\\3 - 2x-12 = 11\\\\-2x-9 = 11\\\\add \ 9 \ to \ both \ sides\\\\-2x-9+9 = 11+9\\-2x = 20\\\\x = -20/2\\\\x = -10](https://img.qammunity.org/2021/formulas/mathematics/college/e39jntroomd6yv05xqwo7okdqre08li6ur.png)
Hence her other solution of x is -10