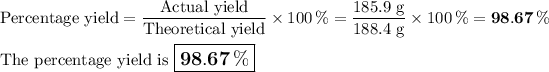Question

Chromium is dissolved in sulfuric acid according to the following equation: Cr + H2SO4 ⇒ Cr2 (SO4) 3 + H2

a) How many grams of Cr2 (SO4) 3 can be obtained by reacting 165 g of 85.67% H2SO4 of purity?

b) If 485.9 g of Cr2 (SO4) 3 are obtained, what is the yield of the reaction?

Answer 1

`\large \boxed{\text{a)188.4 g; b) 98.67 $\, \%$}}`

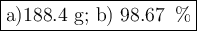
Step-by-step explanation:

We will need a balanced chemical equation with masses and molar masses, so, let's gather all the information in one place.

Mᵣ: 98.08 392.18

2Cr + 3H₂SO₄ ⟶ Cr₂(SO₄)₃ + 3H₂

To solve the stoichiometry problem, you must

• Use the molar mass of H₂SO₄ to convert the mass of H₂SO₄ to moles of H₂SO₄
• Use the molar ratio to convert moles of H₂SO₄ to moles of Cr₂(SO₄)₃
• Use the molar mass of Cr₂(SO₄)₃ to convert moles of Cr₂(SO₄)₃ to mass of Cr₂(SO₄)₃

a) Mass of Cr₂(SO₄)₃

(i) Mass of pure H₂SO₄

`\text{Mass of pure} = \text{165 g impure} * \frac{\text{85.67 g pure} }{\text{100 g impure}} = \text{141.36 g pure}`

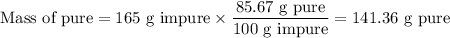
(ii) Moles of H₂SO₄

`\text{Moles of H$_(2)$SO}_(4) = \text{141.36 g H$_(2)$SO}_(4) * \frac{\text{1 mol H$_(2)$SO}_(4)}{\text{98.08 g H$_(2)$SO}_(4)} = \text{1.441 mol H$_(2)$SO}_(4)`

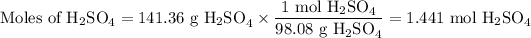
(iii) Moles of Cr₂(SO₄)₃

The molar ratio is 1 mol Cr₂(SO₄)₃:3 mol H₂SO₄
`\text{Moles of Cr$_(2)$(SO$_(4)$)}_(3) = \text{1.441 mol H$_(2)$SO}_(4) * \frac{\text{1 mol Cr$_(2)$(SO$_(4)$)}_(3)}{\text{3 mol H$_(2)$SO}_(4)} = \text{0.4804 mol Cr$_(2)$(SO$_(4)$)}_(3)`

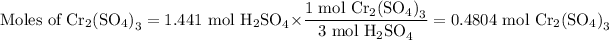
(iv) Mass of Cr₂(SO₄)₃
`\text{Mass of Cr$_(2)$(SO$_(4)$)}_(3) = \text{0.4804 mol Cr$_(2)$(SO$_(4)$)}_(3) * \frac{\text{392.18 g Cr$_(2)$(SO$_(4)$)}_(3)}{\text{1 mol Cr$_(2)$(SO$_(4)$)}_(3)} = \textbf{188.4 g Cr$_(2)$(SO$_(4)$)}_(3)\\\text{The mass of Cr$_(2)$(SO$_(4)$)$_(3)$ formed is $\large \boxed{\textbf{188.4 g}}$}`

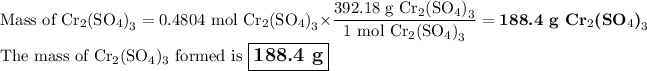
b) Percentage yield

It is impossible to get a yield of 485.9 g. I will assume you meant 185.9 g.

`\text{Percentage yield} = \frac{\text{Actual yield}}{\text{Theoretical yield}} * 100 \, \% = \frac{\text{185.9 g}}{\text{188.4 g}} * 100 \, \% = \mathbf{98.67 \, \%}\\\\\text{The percentage yield is $\large \boxed{\mathbf{98.67 \, \%}}$}`